The domain and range are the intervals in which the function is defined in the x and y axes Answer and Explanation 1 We are given the function {eq}f(x)=2x^23x1 {/eq} Given f(x) = 2–x −5 To find the domain and range of function Explanation So the domain of a function consists of all the first elements of all the ordered pairs, ie, x, so we have to find the values of x to get the required domain Given, f(x) = 2–x −5 Now x is defined for all real numbers Hence the domain of f is R And the range of a function consists of all the second Stack Exchange network consists of 178 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack Exchange
Use The Graph Of The Function To Find The Domain And Chegg Com
Domain and range of f x 2 x
Domain and range of f x 2 x-F (x) = x f ( x) = x The domain of the expression is all real numbers except where the expression is undefined In this case, there is no real number that makes the expression undefined Interval Notation (−∞,∞) ( ∞, ∞) Set Builder Notation {xx ∈ R} { x x ∈ ℝ } The absolute value expression has a V shape 1 Confirm that you have a quadratic function A quadratic function has the form ax 2 bx c f (x) = 2x 2 3x 4 The shape of a quadratic function on a graph is parabola pointing up or down There are different methods to calculating the range of a function depending on the type you are working with



How Do You Find The Domain And Range Of T 1 3 Socratic
Explanation f (x) is a quadratic equation and any values of x will give a real value of f (x) Your domain is {x − ∞ ≤ x ≤ ∞} Hence you minimum point is (3, −1) It is a minimum point because the graph is a "u" shape (coefficient of x2 is positive) df (x) dx = 2x − 6The domain is x 2, infinity) square root of a negative number is not allowed The range is y 0, infinity) EdState the domain and range of f(x) if h(x) =f(x) g(x) and h(x) = 2x2x 2 when g(x) = 2x 4 Select one O a XER, yER Ob XER, yS 7 8 OC XS , YS 7 8 Od XS ,
Doman= R,Range= (−∞,2 Given f (x)= 2−∣x−5∣ Domain of f (x) is defined for all real values of x Since, ∣x−5∣ ≥0 −∣x−5∣ ≤0 2−∣x−5∣ ≤2 f (x) ≤2 Hence, range of f (x) is (−∞,2Write the Domain and Range of the Function F ( X ) = X − 2 2 − X CBSE CBSE (Science) Class 11 Textbook Solutions Important Solutions 9 Question Bank Solutions 9938 Concept Notes & Videos 580 Syllabus Advertisement Remove all ads Write the Domain and Range of the Function F ( X ) = X − 2 2 − XThis would include all values that you can input as x in order to make this problem work The domain of a function is usually all real numbers The range of f(x)=2^x would be the y values This would include all values that would be the output for the y value An example of this would be if you used 2 as x then the function would read f(x)=2^2
Find the Domain and Range f(x)=x^3 The domain of the expression is all real numbers except where the expression is undefined In this case, there is no real number that makes the expression undefined Interval Notation SetBuilder Notation The range is the set of all valid values All these are real values Here value of domain (x) can be any real number Hence, Domain = R (All real numbers) We note that that Range f (x) is 0 or negative numbers, Hence, Range = (−∞, 0 Ex 23, 2 Find the domain and range of the following real function (ii) f (x) = √ ( (9 −x^2)) It is given that the function is a real function Hence, both its domain and range should be real numbers x can be a number from –3 to 3 f (x) is between 0 & 3 Hence, Domain = Possible values of x The domain is the range of x values which give f (x) a value that is unique, such there is only one y value per x value Here, since the x is on the bottom of the fraction, it cannot have any value such that the whole denominator equals zero, ie d(x) ≠ 0 d(x) = denominator of the fraction that is a function of x x − 2 ≠ 0 x ≠ 2




Consider The Function F X X 1 C 2x 8 2x 8 C X 1 Statement 1 Domain Of F X Is Singleton Statement 2 Range Of F X Is Singleton




Domain And Range F X Root 5 6x X2 Maths Relations And Functions Meritnation Com
Find the Domain and Range f (x)=x^2 f (x) = x2 f ( x) = x 2 The domain of the expression is all real numbers except where the expression is undefined In this case, there is no real number that makes the expression undefined Interval Notation (−∞,∞) ( ∞, ∞) Set Builder Notation {xx ∈ R} { x xPutting it all together, this statement can be read as "the domain is the set of all x such that x is an element of all real numbers" The range of f(x) = x 2 in set notation is R {y y ≥ 0} R indicates range When using set notation, inequality symbols such as ≥ are used to describe the domain and range f (x)= x^2 5 The domain are all x values that has images As you see, we do not have any restrictions on the values of x ==> Therefore, the domain is




Find The Domain And Range Of The Function F X 1 1 X 2 X In R X 1 Dot Youtube



Find Domain And Range Of Function Y 1 X Youtube
How to Find the Domain and Range of f(x, y) = ln(xy 2)If you enjoyed this video please consider liking, sharing, and subscribingYou can also help supportInformally, if a function is defined on some set, then we call that set the domain The values taken by the function are collectively referred to as the range For example, the function x2 x 2 takes the reals (domain) to the nonnegative reals (range) The domain and range of the linear function y = 2 (3x) = 6x are (∞, ∞) The domain of 2^ (3x) or of 2·3^x is (∞, ∞)) and the range of these exponential functions is (0, ∞)



Domain Range A Function
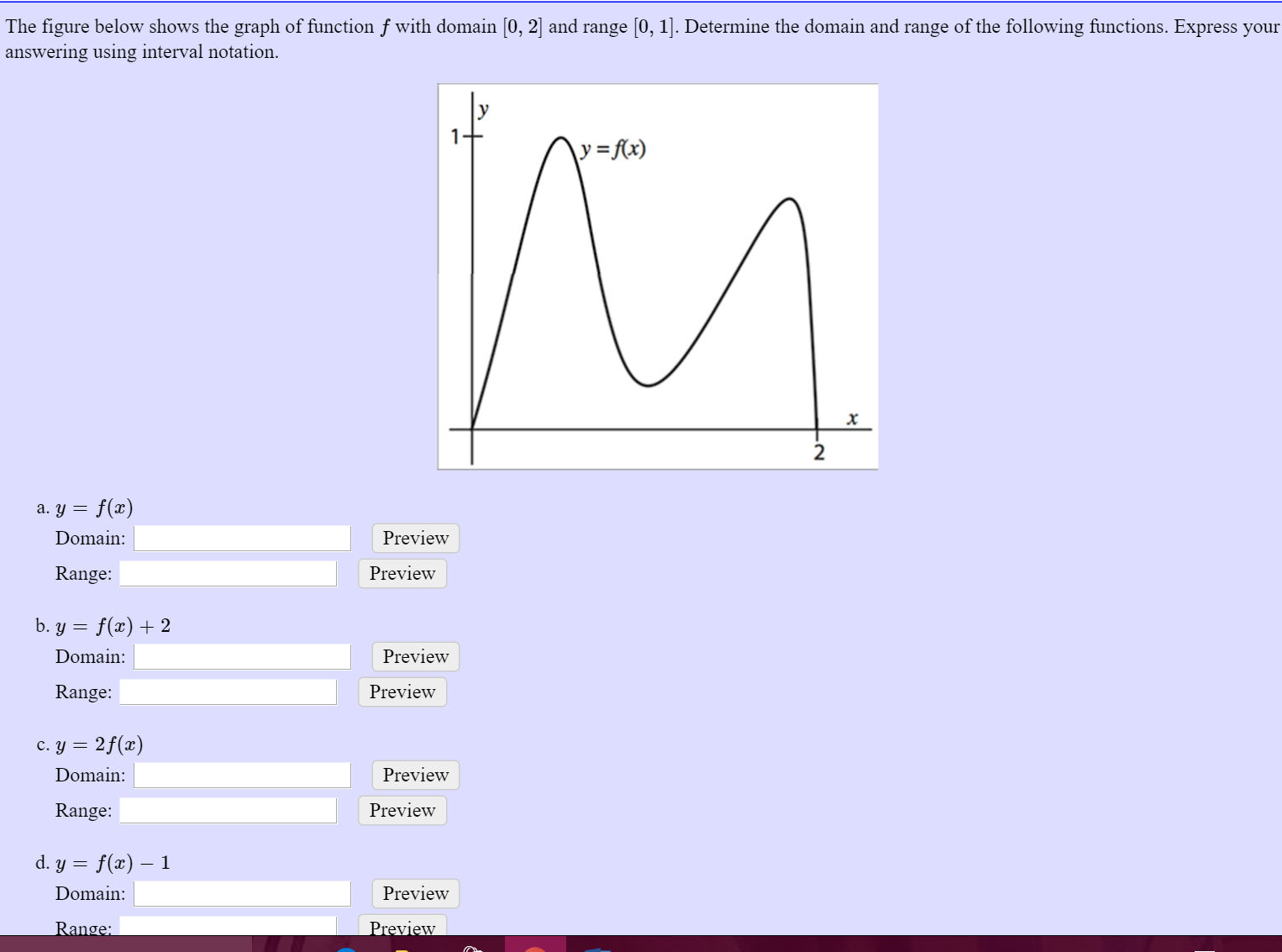



The Figure Below Shows The Graph Of Function F With Chegg Com
We have f(x) = (x 2 9)/(x 3) Domain off Clearly f(x) is not defined for x – 3 = 0 ie x = 3 Therefore, Domain (f) = R – {3} Range off Let f(x) = y Then, f(x) = y (x 2 9)/(x 3) = y x 3 = y It follows from the above relation that y takes all real values except 6 when x takes values in the set R – {3} Therefore, Range (f Consider the function, f(x) = x^2 5 The domain is the set of all possible values of x for which this function is defined For f(x) to be real valued, all real values of x are consistent with the definition of f(x) Thus, domain is R, the set of real numbers The range in this case is also R since it is a real valued function Another thing that might be added is that the codomain which is the set of values in the range R to which elements of the domain are mapped Well, for any value of x f (x) = √x2 − 4 The best and fastest way is to learn how do parental functions look like and how does the formula look like and then use it The domain square root must be greater or equal to 0 x2 −4 ≥ 0 ⇒ (x −2)(x 2) ≥ 0 That happens only when f (x)>0everything that is above x axis, like this (i usually draw a simple picture of quadratic function)
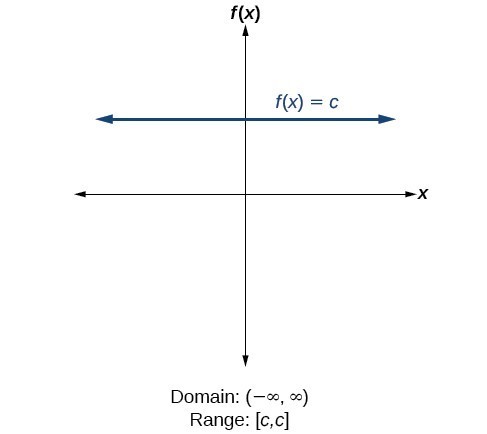



Find Domains And Ranges Of The Toolkit Functions Math 1314 College Algebra
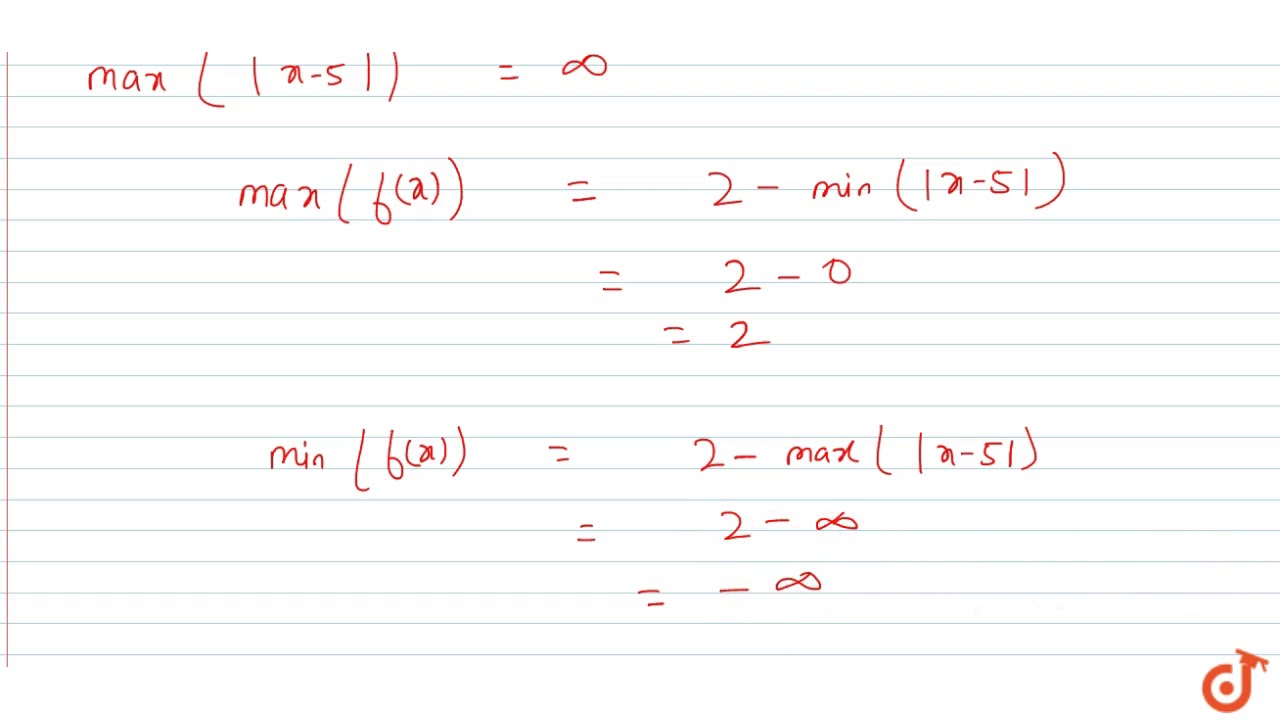



The Domain And Range Of The Function F Given By F X 2 X 5 Is Youtube
Click here👆to get an answer to your question ️ Find the domain and range of √(4x x^2)Domain and Range of Exponential and Logarithmic Functions Recall that the domain of a function is the set of input or x values for which the function is defined, while the range is the set of all the output or y values that the function takes A simple exponential function like f(x) = 2x has as its domain the whole real line Find the domain and range of the function f(x)=x^29/x3 2 See answers Advertisement Advertisement RoseAmber RoseAmber Given function is f(x)=x2−9x−3 since the denominator can not be zero x−3≠0⇒x≠3 the domain of the function is R−{3}




Solved How To Find Domain And Range Of Function X 2 16 X 4 Brainly In



Find The Domain And Range Of The Real Function F X X 2 9 Sarthaks Econnect Largest Online Education Community
The domain is x in RR The range is y in (0,1 The denominator is =1x^2 AA x in RR, 1x^2>0 Therefore, The domain of f(x) is x in RR To determine the range, proceed as follows y=1/(1x^2) y(1x^2)=1 yyx^2=1 yx^2=1y x^2=(1y)/y x=sqrt((1y)/y) The range of f(x) is the domain of x ((1y)/y)>0 y in RR _^("*") 1y>=0 yFind Domain and Range of real functions (1) `f(x)=(x2)/(3x)` (2)`f(x)=1/sqrt(x5)` (3) `f(x)=x/(1x^2)` F x x2 5 f x x 2 5 Domain and range of f(x)=x^25 The domain of the expression is all real numbers except where the expression is undefined What is the domain and range of the function fx 2514 4 Explain Real valued function with some examples 0 R




Find The Range Of Each Of The Following Functions F X X 3 F X 1 X 2 F X X 4 Youtube
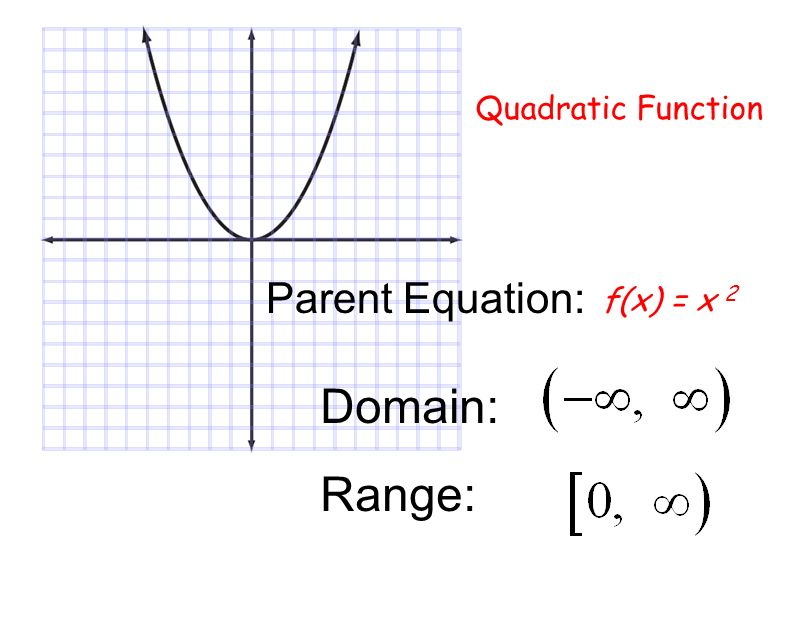



Parent Functions Constant Function Linear Identity Absolute Value Ppt Video Online Download
x >= 3 or in interval notation 3, oo) Given F(x) = sqrt(x 3) A function starts out having a domain of all Reals (oo, oo) A square root limits the function because you can't have negative numbers under the square root (they are called imaginary numbers) This means " "x 3 >= 0 Simplifying " "x >= 3Domain and Range A function in two variables can be expressed as {eq}y=f(x) {/eq} where {eq}x {/eq} is the independent variable and {eq}y {/eq} is the dependent variableRange The out comes or values that we get for y is known as range Domain for given function f (x) = x 3 For any real values of x, f (x) will give defined values Hence the domain is R Since we have absolute sign, we must get only positive values by applying any positive and negative values for x in the given function




Find The Domain And Range Of The Function F X Y Chegg Com




Domain And Range Shortcut Rules The Qubits Blog
Click here👆to get an answer to your question ️ Find the domain and the range of the real function f(x) = √(9 x^2)F (x) = 1 6 − x 2 For domain under root should not be n egative quantity, 1 6 − x 2 ≥ 0 1 6 ≥ x 2 Therefore, x ≤ 4 or x ≥ − 4 Then, The domain − 4, 4Click here👆to get an answer to your question ️ Find the domain and range of the function f (x) = x ^2/1 x ^2 Join / Login > 11th > Applied Mathematics > Functions > Introduction of functions




If The Function F X Has A Domain Of 2 X 8 And A Range Of 4 Y 6 And The Function G X Is Defined By The Formula G X 5f 2x Then What Are




Domain And Range Of Quadratic Functions Video Khan Academy
Answer and Explanation 1 Given f(x) = 1 x f ( x) = 1 x Domain Since the function is a fraction, the value of the variable are all real numbers except 0 0 since it will result to an undefinedF(x)=1 if x4>0 f(x)=1 if x4F is increasing on 2,0 and decreasing on 0,2 So since f is continuions and différentiable on its domain It has a maximum for x=0 and a minimum at x=2 or 2 and since both f(2) and f(2) are equal to each other, the minimum is f(2)=f(2)=0 The maximum is at x=0 where f(x)=2 so the range is 0;2




Find The Domain And Range Of The Function F R To R F X X 2 1



Domain And Range Boundless Algebra
Precalculus questions and answers Determine the domain of each of the following functions (a) f (x)= X2 x5 Determine the range of this function by taking the inverse of it and then taking the domain of the inverse which is going to be the range of the f (x) Question Determine the domain of each of the following functionsTo ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW Find domain and range of `f(x)=x/(1x^2)`F (x)=sqrt (x2) Answer by edjones (8007) ( Show Source ) You can put this solution on YOUR website!



Q Tbn And9gcqj529kunx E23asbmwgf8sdjnucswezuevva8edino5czgfbjv Usqp Cau




Introduction To Function Domain And Range Mohd Noor
Precalculus Find the Domain and Range f (x)=x^22x2 f (x) = x2 − 2x − 2 f ( x) = x 2 2 x 2 The domain of the expression is all real numbers except where the expression is undefined In this case, there is no real number that makes the expression undefined Interval NotationFind the Domain and Range f (x)=3x2 f (x) = 3x − 2 f ( x) = 3 x 2 The domain of the expression is all real numbers except where the expression is undefined In this case, there is no real number that makes the expression undefined Interval NotationFor the domain, it has to be that 4x^2 >0 so 2




Find The Domain And Range Of The Function F X 1 2 Sin3x Youtube




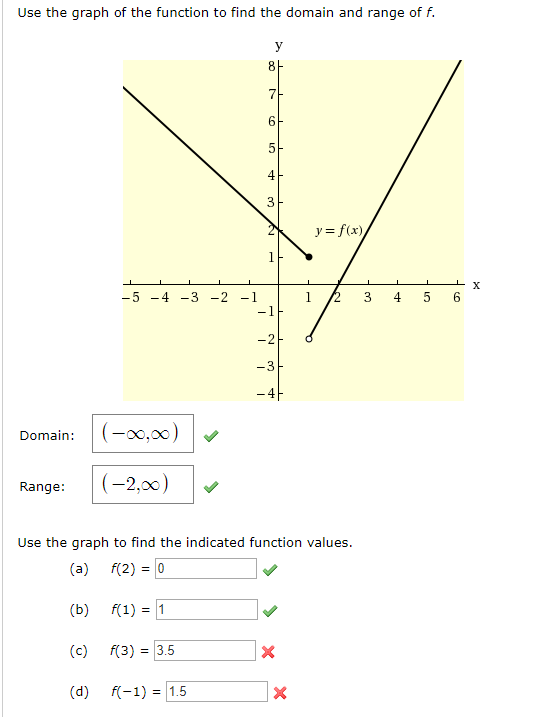
Use The Graph Of The Function To Find The Domain And Chegg Com
Find the Domain and Range f(x)=2/x Set the denominator in equal to to find where the expression is undefined The domain is all values of that make the expression definedThe domain is all real numbers, and the range is all real numbers f(x) such that f(x) ≤ 4 You can check that the vertex is indeed at (1, 4) Since a quadratic function has two mirror image halves, the line of reflection has to be in the middle of two points with the same y valueFind the Domain and Range F (x)=1/ (x^2) F (x) = 1 x2 F (x) = 1 x 2 Set the denominator in 1 x2 1 x 2 equal to 0 0 to find where the expression is undefined x2 = 0 x 2 = 0
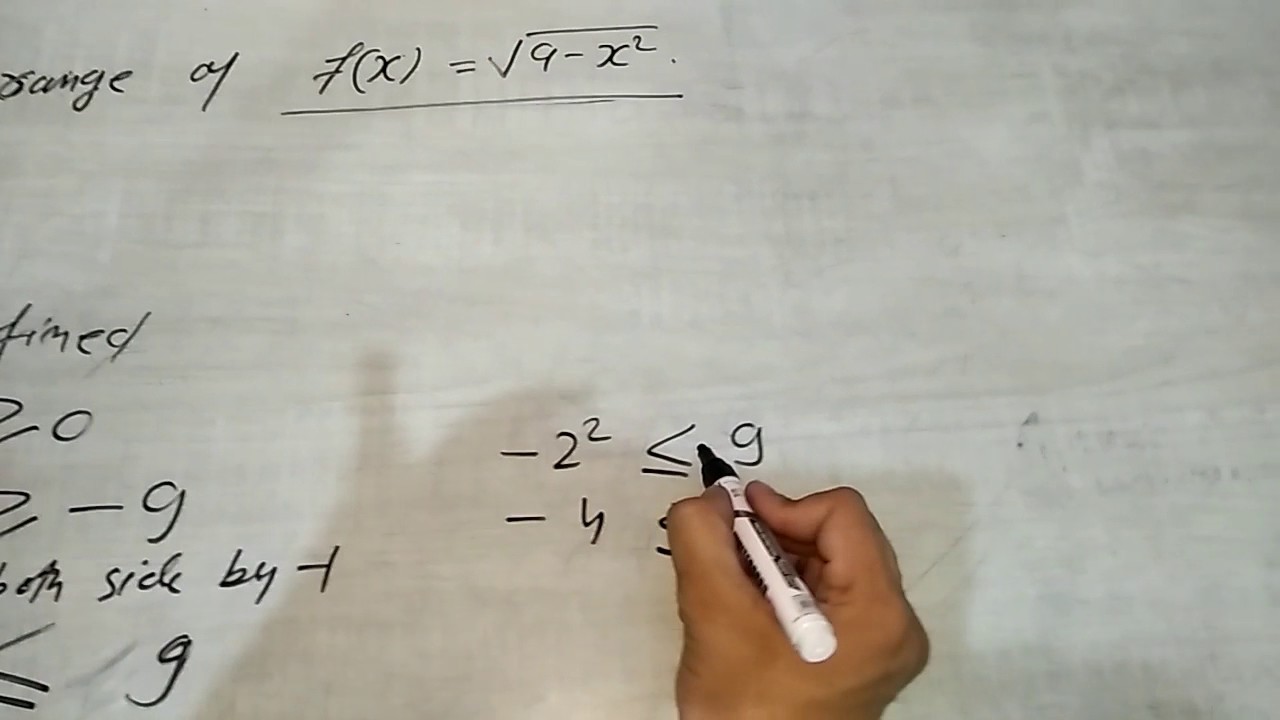



11th Domain And Range Of Squre Root Of 9 X2 Youtube



Solution What Is The Domain And Range Of F X 10 X 2




Find The Domain And Range Of F X 3 2 X 2 Brainly In



Draw The Graph Of The Function F X X 2 And Write Its Domain And Range Sarthaks Econnect Largest Online Education Community
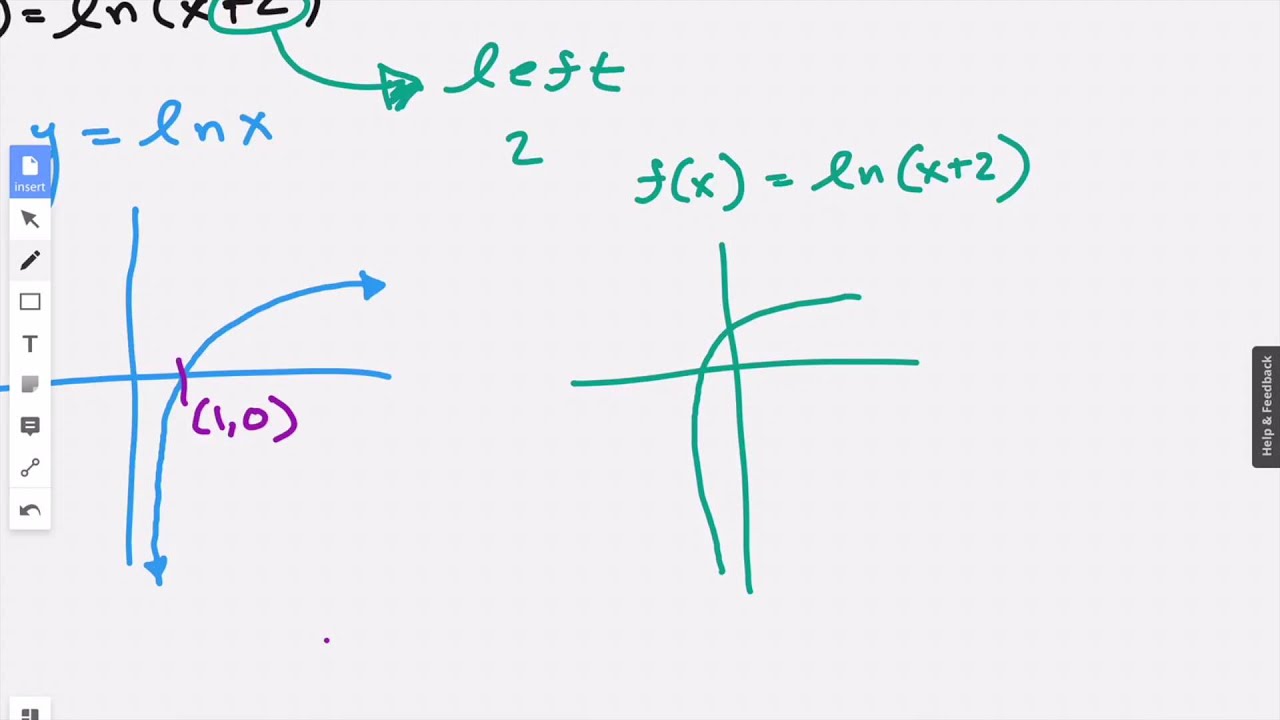



What Is The Domain And Range Of The Function Fx Lnx 2 Youtube



Domain And Range




Misc 4 Find Domain And Range Of F X Root X 1 Chapter 2
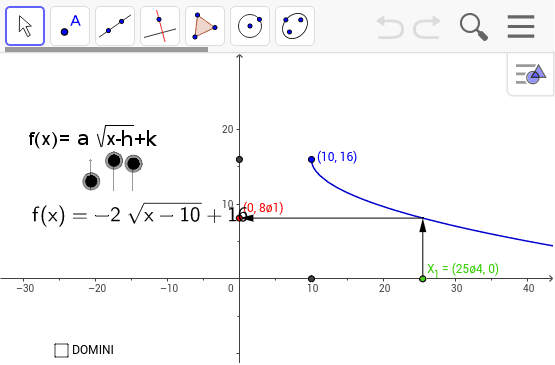



Domain And Range Of The Function F X A Sqrt X H K Geogebra



Q Tbn And9gcqnlzmdu7bo39sbnyy8n Qw7ju Qltdhgbmznxvwuughbwlyozz Usqp Cau



Consider The Following Function F X Ln X 7 Chegg Com



Domain And Range




Graph F 1 X Identify The Domain And Range Of Chegg Com



F X X 2 4 A Use A Graphing Calculator To Draw Chegg Com
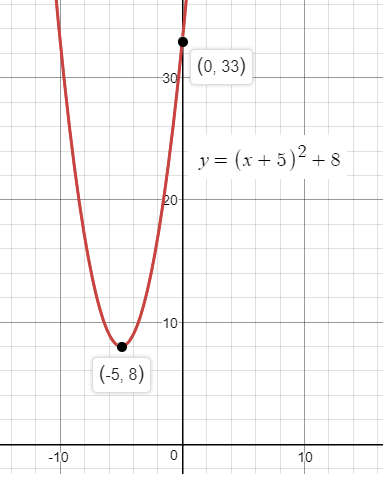



How Do You Find The Domain And Range Of F X X 5 2 8 Socratic




Find The Domain And The Range Of The Function F X X 2 25 X 5 Youtube




If F X X 2 X X 2 2x Then Find The Domain And Range Of F Show That F Is One One Youtube



Problem 9 Let F X 2 3x4 On The Largest Domain For Which The Formula Makes Sense A Find The Domain And Range Of F X Then Sketch The Graph Course Hero




Find The Domain And Range Of The Function F X 1 1 X 2 X In R X 1 Dot




Find The Domain Range Of F X 1 9 X 2 Brainly In
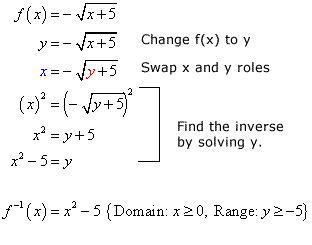



Inverse Of Square Root Function Chilimath
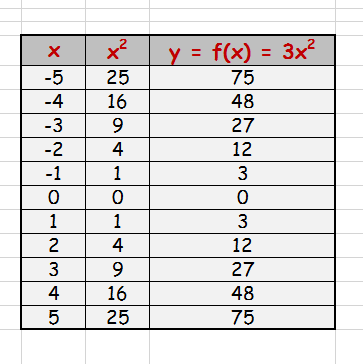



How Do You Find The Domain And Range Of Y 3x 2 Socratic




Find The Domain And Range Of The Function F X Sin 1 X 2 2




Find Domain And Range Of Real Functions 1 F X X 2 3 X 2 F X 1 Sqrt X 5 Youtube




Find The Domain And Range Of The Real Function Defined By F X X 2 1 X 2 Show That F Is Many One
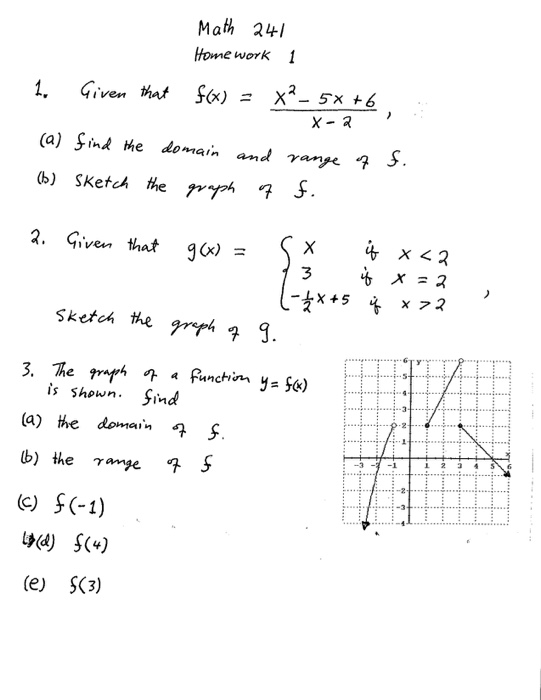



1 Given That F X X 2 5x 6 X 2 A Find The Domain Chegg Com




Misc 5 Find Domain And Range Of F X X 1 Class 11




The Problem Was To Graph The Function Find The Chegg Com




Find The Domain And Range Of The Real Function Fx 1 1 X 2 Brainly In




Find Domain And Range Of F X 1 16 X 2 Brainly In




Graph The Function And State The Domain And Range Chegg Com



Domain And Range Of A Function




Domain And Range Of Quadratic Functions Video Khan Academy




Find The Domain Of The Range Of Each Of The Following Real Functions F X X 2 16 X 4




Find The Domain Range Of F X 1 Square Root Of 9 X2 Maths Relations And Functions Meritnation Com




Find The Domain And Range Of F X Sqrt 16 X 2 Mathematics Stack Exchange




6 Ways To Find The Domain Of A Function Wikihow
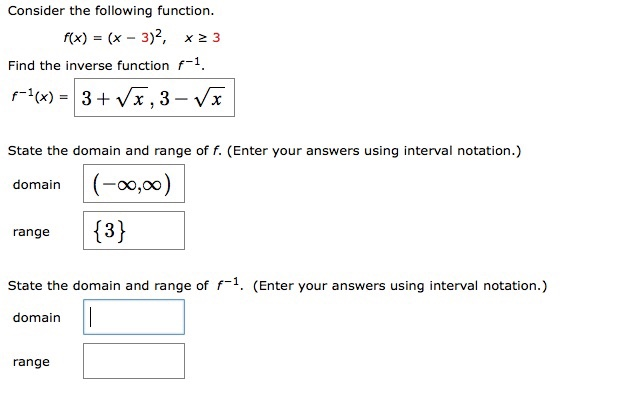



Consider The Following Function F X X 3 2 X 2 3 Chegg Com
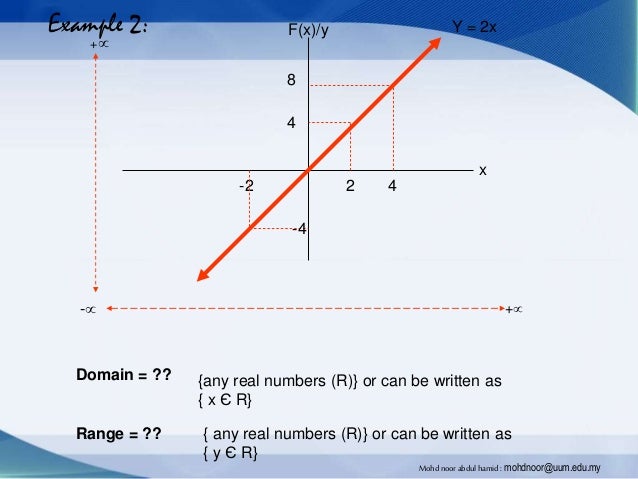



Introduction To Function Domain And Range Mohd Noor
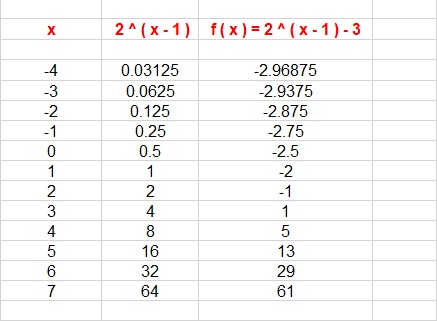



How Do You Graph F X 2 X 1 3 And State The Domain And Range Socratic



The Domain And Range Of The Function F X X 2 Is Donimain
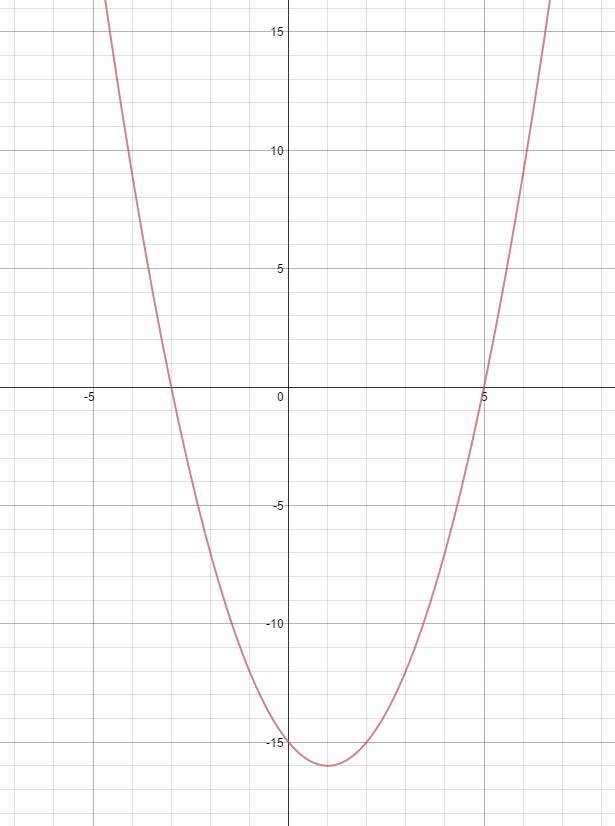



How Do You Find Domain And Range For F X X 2 2x 15 Socratic



3
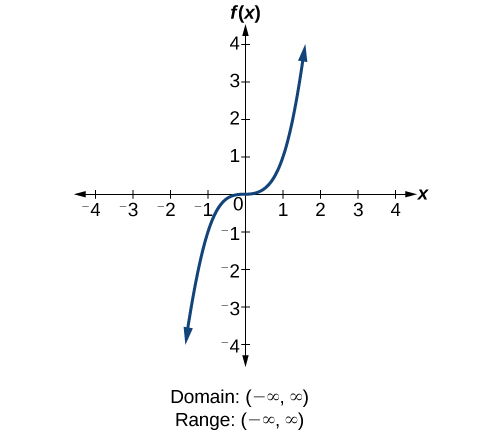



3 2 Domain And Range Mathematics Libretexts




Find The Domain And Range Of The Real Function Defined By F X X 2 1 X 2 Show That F Is Many One




F X Square Root Of X 2 16 Find Domain And Range Brainly In
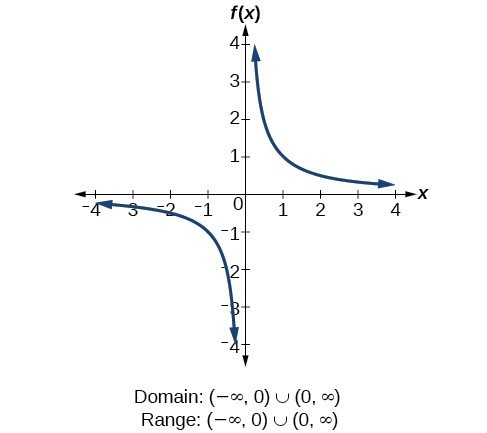



Determine Domain And Range From A Graph College Algebra




Find Domain And Range Of X 2 9 X 3 Brainly In




Find The Domain And Range Of The Real Function F X Sqrt 9 X 2 Youtube



How Do You Find The Domain And Range Of Y Sqrt 3x 5 Socratic
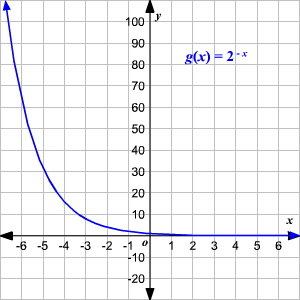



Domain And Range Of Exponential And Logarithmic Functions
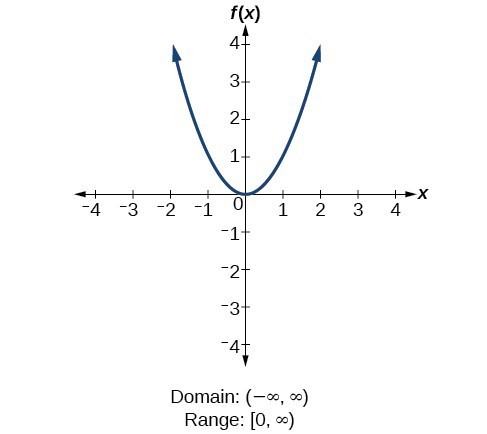



Determine Domain And Range From A Graph College Algebra



Find Domain And Range Of 1 9 X 2 Dumians



Search Q Domain And Range Of 1 2bx 5e2 Tbm Isch
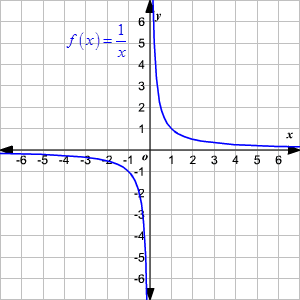



Domain And Range Of Rational Functions




Find The Domain And Range Of F X Sqrt 16 X 2 Mathematics Stack Exchange
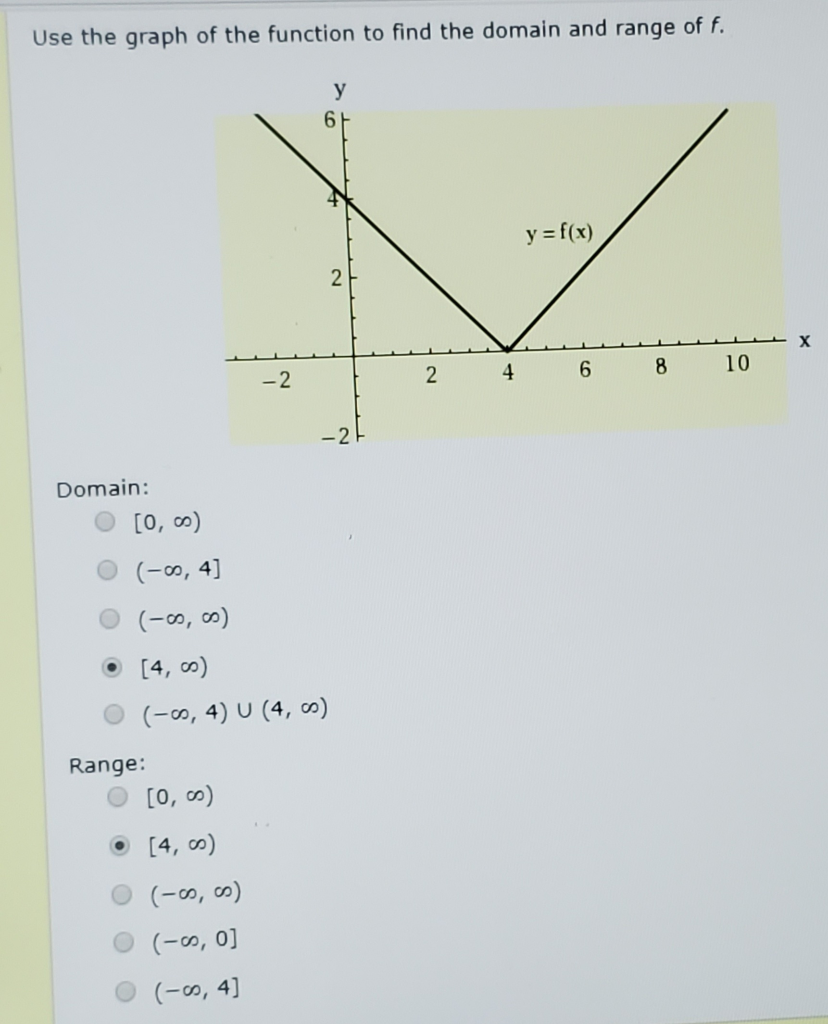



Use The Graph Of The Function To Find The Domain And Chegg Com




Find The Range F X Root 9 X 2 My Doubt Is That The Answer Says 0 3 But Since We Have A Square Root Won 39 T We Get Range 3 3 Mathematics Topperlearning Com Zmdkzt22
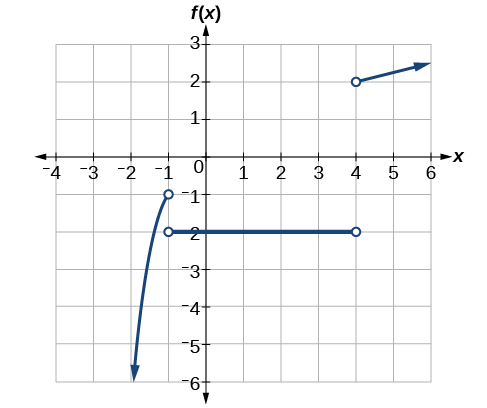



3 2 Domain And Range Mathematics Libretexts




Finding Domain And Range



Solution Find The Range Of F X X 2 2x 1 Determine The Values Of X In The Domain Of 39 F 39 For Which F X 2 2 Means Squared
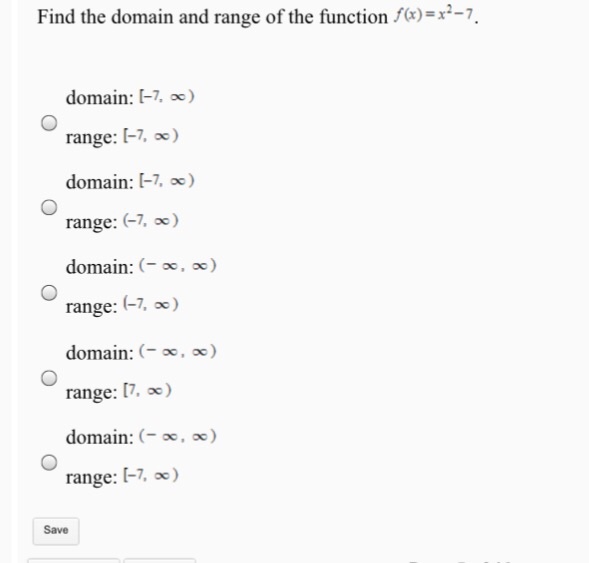



Find The Domain And Range Of The Function F X X2 Chegg Com



Domain And Range Ppt Download
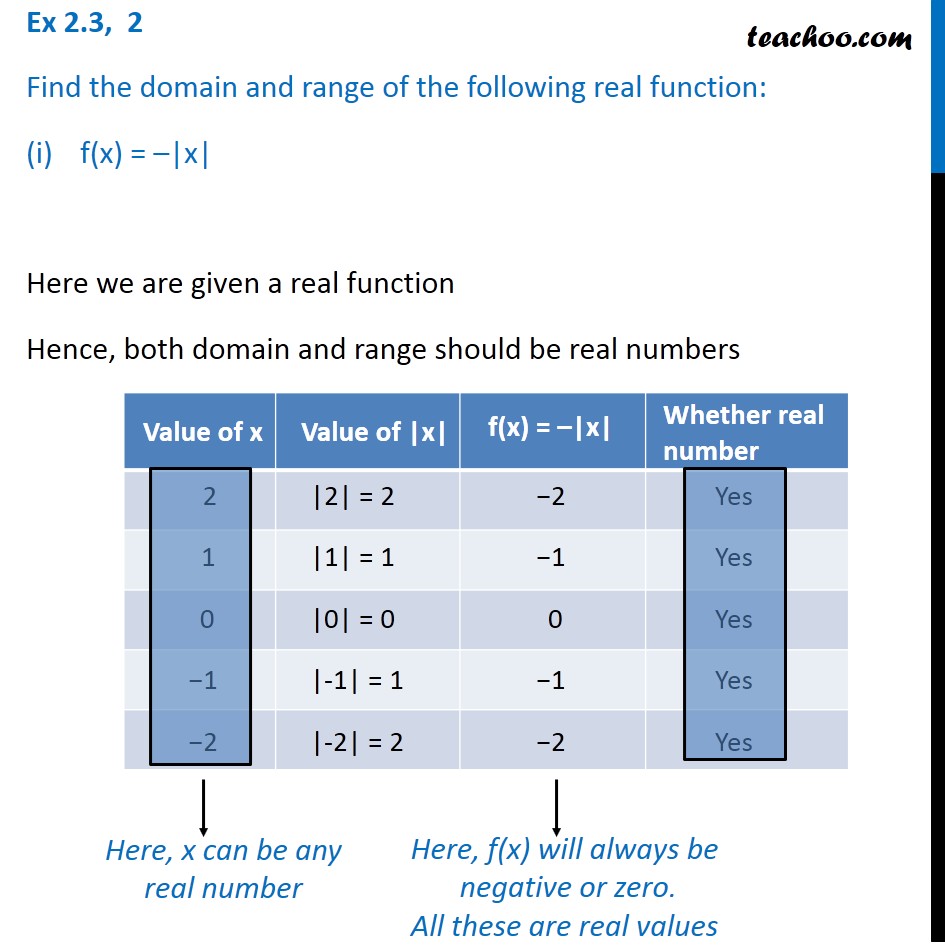



Ex 2 3 2 Find Domain And Range I F X X Chapter 2



For The Function F X X 2 5 Find The Domain And Range Enotes Com




Find The Domain And Range Of The Function F X 16 X 2 Donimain



How Do You Find The Domain And Range Of T 1 3 Socratic
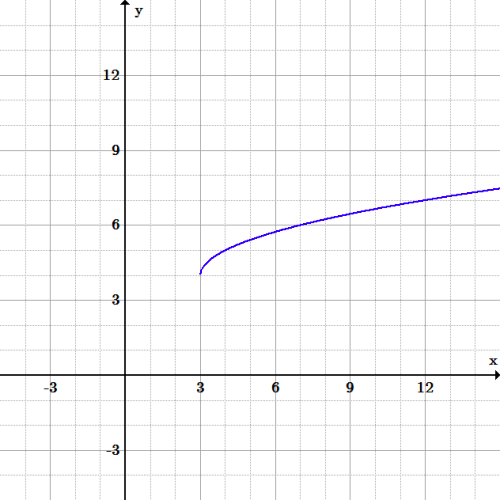



Domain And Range Boundless Algebra




What Is The Domain And Range Of F X Abs X 3 5 2 Socratic




Find The Domain And Range Of The Following Functions I F X X 2 Ii F X X 1 3 X




Find The Domain And Range Of The Function F X X 1 X 2 Brainly In




Find Domain And Range Of Real Functions 1 F X X 2 3 X 2 F X 1 Sqrt X 5 3 F X X 1 X 2




What Is The Domain And Range Of F X X 2 5 Show The Complete Solutions Brainly Ph




Find The Domain And Range Of The Function F X 1 1 X 2 X In R X 1 Dot Youtube
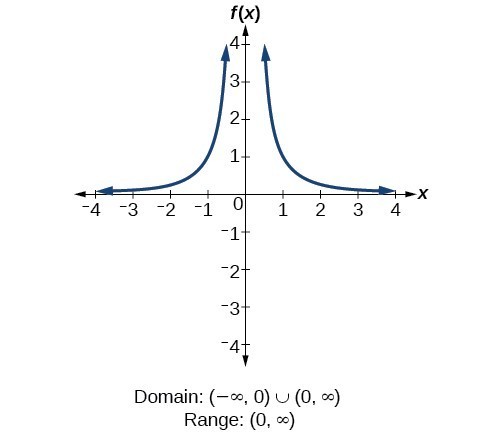



Determine Domain And Range From A Graph College Algebra
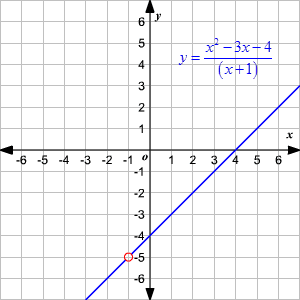



Domain And Range Of Rational Functions




What Is The Domain And Range Of The Function F Given By F X 2 X 5 Mathematics Topperlearning Com Gh19atoo




Domain And Range Of 1 X 2 2x 8 Youtube



What Is The Domain And Range Of F X X 1 X 2 1 X 3 Quora




What Is The Domain And Range Of F X X 2 5 Brainly Ph



What Is The Domain And Range Of X 2 1 X 2 Quora



Domain And Range Examples Domain And Range Of Functions




Find Domain And Range Of Function Y 1 X Youtube



No comments:
Post a Comment